云南工商學院智能科學與工程學院蘇為斌
1 引言
工業六軸機械臂在生產環境中偶發碰撞事故,可能對機器人本體、周邊設備和人員造成損害。隨著智能制造產業的快速發展,國內外有關機器人誤傷人類的報道屢見不鮮。為減少這類事故,通常采用柵欄將人員分隔開來。然而傳統的安全措施不足以應對所有場景,尤其是在人機協作環境中,人類需要在沒有完全隔離的情況下與機器人共同工作,故需要采取更加先進的技術來確保安全性。
智能技術的引入是一種有效的方法。該方法通過提高機器人空間運動的智能化水平,識別和繞開障礙物,有效提高了安全性。然而,長期以來學術界在研究人工智能(artificial Intelligence,AI)時,通常將智能與大腦的思考能力緊密聯系在一起,過多強調算法和算力,常常忽視了具身場景對智能的影響。在實際的生產環境中,智能不僅僅是邏輯推理、數據處理和算法計算的結果,它還涉及到機器人本體在環境中的互動以及由此產生的感知和行為。“具身智能”(embodied Intelligence,EI)要求機器人本體對外界的感知更加類似于人類,而非毫無知覺的鋼鐵。事實上,人類的思維過程和認知功能是根植于身體結構及其與外界交互的動態調整方式之中的。人類的身體,包括感官、運動系統、神經系統等,在促進人類理解世界、展現人類技能以及解決問題方面起著至關重要的作用。若把這種先進的技術應用到工業機器人中,將極大地提高其智能化和安全化水平。
本文基于邊緣計算,以工業六軸機械臂為對象,擬在肘、腕、軸等位置安裝多個先進傳感器,融合多傳感信息,動態捕捉機械臂及末端執行器的三維可達空間(reachable space)、靈巧工作空間(dexterouswork space)和奇異位形(singular configurations)等位置信息,構建齊次空間變換坐標矩陣,動態感知障礙物和人所處的空間位置信息,并基于這些信息,以邊緣計算為基礎平臺,研究和開發能夠靈活避障的具身智算工具,以期促進機械臂智能化和安全化水平的提升。
2 相關研究
EI的概念最早可追溯到1950年,艾倫·圖靈[1]探討了AI發展的兩條路徑:一條是聚焦于抽象計算所需的智能,另一條則是為機器配備傳感器和執行器,使其能夠與環境互動并進行學習。1986年,布魯克斯[2]提出了行為式機器人概念,強調智能是具身化和情境化的體現。2000年左右,羅爾夫·普費弗和克里斯蒂安·謝爾[3]提出智能是行為主體基于整個身體結構和功能的綜合體現。近年來,隨著強化學習技術的快速發展,EI在機器人控制領域得到了廣泛的應用。申鎧瑤、聶一鳴等[4]對比了傳統比例積分微分、滑動模態控制等方法,綜述了基于圖神經網絡和Transformer的EI形態控制方法。陳鉑壘、鐘萍等[5]從計算機視覺識別出發綜述了以物體目標導航為導向的EI架構。北航任磊團隊[6]則把EI提升到了推動智能制造產業發展,并把EI認為是AI的終極表現形式。
可見,EI已再度成為當前AI領域的研究熱點。由于EI強調智能體通過身體與環境的互動產生智能行為,因此需要強大的計算資源來實時處理感知數據、生成交互指令以及執行復雜任務,邊緣計算顯然是EI的最佳支持平臺。然而當筆者以“邊緣計算、具身智能”作為關鍵詞檢索國內外研究文獻時,發現現關研究太少,且這些僅有的文獻大多集中發表于2024年。比如基于云計算與霧計算相互融合的EI框架[7],以及基于斯坦福大學開源機器人ROS框架融合YoloV5的EI控制方法[8]。在國內,鄧三鵬等[9]提出了EI機器人研究存在的問題,并給出了相關建議,然而其文章更加傾向于應用AI大模型及深度學習加強EI研究,對于計算平臺則沒有更多闡述。
盡管EI與邊緣計算結合具有重要的實踐意義,但目前相關研究和應用相對較少,且尚處于起步階段,缺乏系統深入的開發。因此本文以六軸機械臂為實踐對象,以邊緣計算為平臺,提出了一種新型的具身智算平臺。
3 理論分析
六軸機械臂的各個關節旋轉決定了末端執行器在三維空間中的位置和姿態變化。為了將這些關節的旋轉運動轉換為笛卡爾坐標系中的位置和姿態,通常使用正向運動學和逆向運動學來進行計算。
3.1 軸關節運動關系
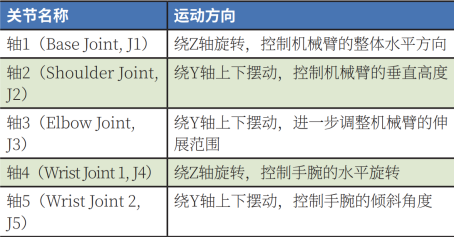
六軸旋轉關系如表1所示。
表1 六軸機械臂軸關節運動方向

3.2 正向運動學與解逆
正向運動學是從給定的關節旋轉角度計算末端執行器在笛卡爾坐標系中的位置和姿態。其具體步驟如下:
(1)齊次變換矩陣:每個關節的旋轉可以表示為一個齊次變換矩陣,該矩陣描述了從一個坐標系到另一個坐標系的變換。假設每個關節旋轉相應角度,則每個關節的變換矩陣Ti可以簡寫表示為式(1):

其中:
Ri是3×3旋轉矩陣,描述了坐標系之間的旋轉關系。
pi是1×3平移位置矩陣,描述了坐標系之間的位移關系。
0是1×3全零矩陣,1是比例變換標量,兩者用于保持齊次坐標的形式。
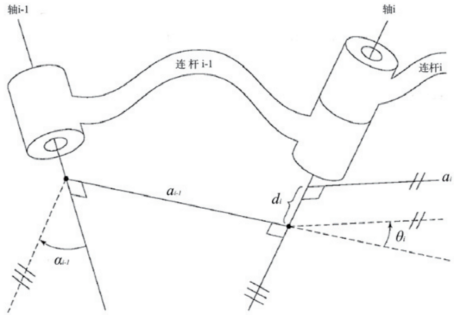
圖1 機械臂的四個D-H參數
這種參數化的方法是由法國工程師雅克·丹納維特(Jacques Denavit)和理查德·哈滕貝格(Richard S.Hartenberg)于1955年提出,簡稱D-H參數[10]。Ri旋轉矩陣和pi位置矩陣由機械臂X軸向連桿長度ai、關節軸線扭角αi、Z軸向偏距di和沿Z軸旋轉偏離X軸的連桿夾角θi構成,其幾何關系如圖1所示。由于六軸機械臂各連桿與軸都呈現為垂直關系,則相對坐標系與參考坐標系在遞推構造Ti時可寫成式(2):
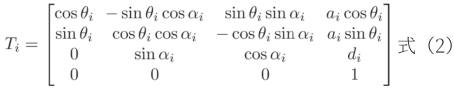
若從機械臂基座開始推導,其變換矩陣T1是相對于J1到J2計算而得,X軸和Z軸平移了一個固定數量,所以a1、d1是一個常數,J2關節與J1關節扭轉了π/2,J2旋轉產生在局部坐標相對于X軸的連桿夾角θ1是一個變量,如表2所示。
接著,從J2到末端執行器可以依次推導出變換矩陣T2~T6所對應的D-H參數,需要注意的是T6是末端執行器的連接法蘭,其每個關節定義的相對座標如圖2所示。
表2 六軸機械臂變換矩陣D-H參數
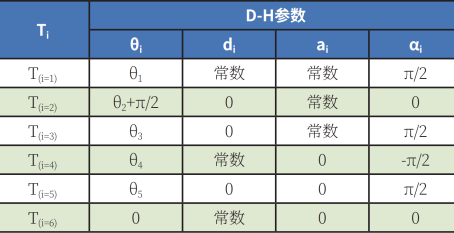
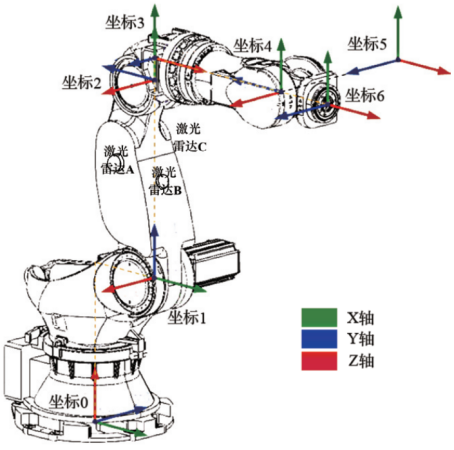
圖2 六機械臂關節坐標定義
(2)串聯變換矩陣:為了得到末端執行器相對于基座的總變換矩陣Tend,需要將所有關節的變換矩陣依次相乘,如式(3):
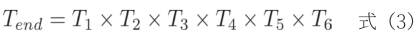
最終的變換矩陣Tend包含了末端執行器在笛卡爾坐標系中的位置pend和姿態Rend信息,可提取出歐拉角(euler angles)、四元數(quaternion)或旋轉矩陣等形式,用于描述末端執行器的姿態。其運算后的矩陣形式表示如式(4):

(3)解逆的增強方法:逆向運動學是從已知末端執行器在笛卡爾坐標系中的位置和姿態,計算出各個關節的角度,計算復雜,且存在多個解或無解的情況。在EI與邊緣計算賦能的架構下,可以通過傳感器感知機械臂各個關節和障礙物所處空間位置。如圖2所示,在機械臂肘部安裝3個小型固態激光雷達,通過邊緣算力解析點云數據便能實現。當然構建EI賦能的傳感器并不限于激光雷達,也可以使用其它觸覺、聽覺、視覺、紅外等高級傳感器。
3.3 空間矩陣融合算法
將激光雷達(LiDAR)的空間矩陣進行融合,可以顯著提高環境感知的精度和可靠性,但通常需要解決以下幾個關鍵問題:坐標系對齊、數據同步、點云配準和融合算法。
(1)坐標系對齊:3個激光雷達的空間位置不同,因此首先需要進行外參標定,以確定它們之間的相對位置。由于3個雷達均安裝于機械臂肘上,具有已知幾何形狀,故可采用靜態標定板法如棋盤格或平面板[11],其優點是結構簡單,對邊緣算力的要求不高。
(2)坐標系轉換:當激光雷達的相對位姿確定后,就可以使用齊次變換矩陣將每個激光雷達的點云數據轉換到一個統一的坐標系中。令激光雷達B為參考坐標系,則肘部兩側的A和C相對于B的變換矩陣分別為TBA和TBC,對于點云矩陣,應考慮A、C雷達鏡像安裝關系及與B的垂直關系。假設變換后,激光雷達A和C的點云數據為PA和PC,則可以通過式(5)轉換到激光雷達B的坐標系中:
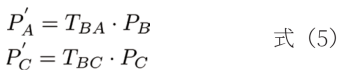
經過齊次變換后,PA(’)、PC(’)和PB三個坐標的點云數據便可處于共同的三維空間。但此時三個雷達數據的視場角會產生數據重疊以及因比例和位置失調造成的偏差,可在機械臂上定義三個絕對物理參考點,且讓三個雷達均掃描到這些點。最后通過絕對角度和距離作為系數進行配準,便可修正三個雷達的比例和位置失調。
(3)加權融合:對于三個雷達的視場角有重疊的情況,根據每個雷達的測量精度和置信度,對重疊區域的點云進行加權平均。通常,距離越近、反射率越高、測量誤差越小的點權重越大。因三個雷達的累加權重未必為1,故加權平均公式為式(6):
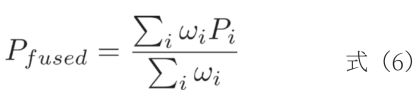
4 系統框架
在完成理論分析后,便可在該理論基礎上搭建系統框架。眾所周知,邊緣計算將業務下沉到靠近控制對象一側,降低了網絡延遲,提高了實時性,故可不用過度依賴遙遠的云計算資源,提高了系統的可靠性和穩定性。這種方式不但為EI提供了及時、高效的算力,而且還為接入各類傳感器提供了泛在的接口。因此邊緣計算是六軸機械臂實現智能化突破的最佳平臺。本文提出的系統框架如圖3所示。
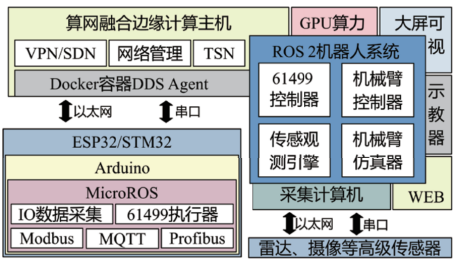
圖3 六軸機械臂具身智算平臺系統框架
該六軸機械臂的EI控制平臺采用ROS2開源操作系統為核心,是一種構建于多臺計算機之上的元操作系統[12]。本框架給出了六種計算機,分別是算網融合主機、GPU算力主機、數據可視化主機、機器人示教器編程主機、WEB服務器和高級傳感器采集計算機。其中,算網融合主機既是路由器,用于負責連接各臺主機、保障網絡安全和管理網絡地址,又是虛擬網絡VPN/SDN和時間敏感網絡TSN的管控中心,還是嵌入式采集器的代理容器,是上下層系統無縫連接的關鍵環節。
由ESP32或STM32開發的嵌入式控制器,在Arduino框架之上通過集成MicroROS,負責模擬量和開關量的數據采集與輸出控制。IEC61499實現了嵌入式端與ROS2內核的映射,并開發了常用工業通信協議如Modbus、Profibus和物聯網MQTT通信等。
ROS2把所有涉及六軸機械臂的計算單元無縫關聯到了一起,使原本分離的計算機變成了一個整體。在ROS2之上開發的機器人節點分布在最合適的計算機上各司其職,針對機械臂開發IEC61499控制器、機械臂控制器、傳感器的觀測引擎和機械臂的仿真器等。
5 總結和展望
本文針對工業六軸機械臂,分析了坐標變換和坐標融合的理論方法,給出了一種針對機械臂具身智算平臺的邊緣計算系統框架方案。未來,將通過搭建該具身智算平臺,代替六軸機械臂的傳統模式,提升人機協作水平。計劃在2026年完成平臺建設,成功開發EI賦能的新型機械臂,顯著提高智能化水平。
未來,延續本文思路,將實現一項應用場景試點。比如在搬運碼垛場景,工程師只需向機器人指定任務的源頭和搬運目標,接著通過口頭語音、手勢、圖片等對工作任務進行描述,機械臂在認清所需搬運物資的形狀、顏色、數量和大概尺寸信息后,便能自動選用夾具、生成導航路徑和自動完成搬運、堆垛、碼放等。此外,在機械臂的運動軌跡上將實時生成避障策略,防止碰撞事故發生。
作者簡介:
蘇為斌(1983-),男,云南通海人,副教授,博士,現任教于云南工商學院智能科學與工程學院,主要研究方向為邊緣計算、工業自動化、人工智能等。
參考文獻:
[1] Turing A M. Computing machinery and intelligence[M]. Springer Netherlands, 2009.
[2] Brooks R. A robust layered control system for a mobile robot[J]. IEEE journal on robotics and automation, 1986, 2 (1) : 14 - 23.
[3] Pfeifer R, Scheier C. Understanding intelligence[M]. MIT press, 2001.
[4] 申鎧瑤, 聶一鳴, 商爾科, 等. 具身智能形態控制方法綜述[J]. 智能安全, 2024, 3 (1) : 74 - 84.
[5] 陳鉑壘, 康嘉緒, 鐘萍, 等. 面向具身人工智能的物體目標導航綜述[J/OL]. 軟件學報, 1-43 [2025-01-06].
[6] Ren L, Dong J, Liu S, et al. Embodied Intelligence Toward Future Smart Manufacturing in the Era of AI Foundation Model[J]. IEEE/ASME Transactions on Mechatronics, 2024.
[7] Hu D, Lan D, Liu Y, et al. Embodied AI Through Cloud-Fog Computing: A Framework for Everywhere Intelligence[C]//2024 IEEE 33rd International Symposium on Industrial Electronics (ISIE). IEEE, 2024 : 1 - 4.
[8] Gan Y, Zhang B, Shao J, et al. Embodied Intelligence: Bionic Robot Controller Integrating Environment Perception, Autonomous Planning, and Motion Control[J]. IEEE Robotics and Automation Letters, 2024.
[9] 鄧三鵬, 張香玲, 王凱, 等. 具身智能機器人關鍵技術及發展趨勢研究[J]. 裝備制造技術, 2024, (6) : 2 - 10.
[10] Denavit J, Hartenberg R S. A kinematic notation for lower-pair mechanisms based on matrices[J]. Journal of Applied Mechanics, 1955, 22 (2) : 215 - 221.
[11] Zhang Z. A flexible new technique for camera calibration[J]. IEEE Transactions on pattern analysis and machine intelligence, 2000, 22 (11) : 1330 - 1334.
[12] 蘇為斌. 論邊緣計算元操作系統[J]. 自動化博覽, 2024, 41 (2) : 59 - 63.
摘自《自動化博覽》2025年2月刊






 資訊頻道
資訊頻道